Ed25519 是一个基于椭圆曲线的数字签名算法,它高效,安全且应用广泛。TLS 1.3, SSH, Tor, ZCash, WhatsApp 和 Signal 中都使用了它。本文主要讲解以下几点:
1. 介绍一点群论知识,目的是让大家对 Ed25519 和其可延展性问题的原理有一种直觉。若想深入理解,还需参考其他资料;
2. 针对 rust 库 ed25519-dalek 的 1.0.1 版本讲解 ed25519 的实现;
3. 针对该库的延展性问题做出解释。
数学要点回顾
群的定义与性质
群论是抽象代数研究的内容,但抽象代数的一些思想是程序员非常熟悉的。面向对象中的继承就是一个很好的例子,我们都知道子类继承了父类后,就能使用父类中定义的方法。可以将抽象代数理解为对一个抽象的数据结构定义了一些性质,由这些性质推导出来的定理对于所有的子类都成立。
慢雾:JPEG'd攻击者或已将全部6106.75枚ETH归还给项目方:8月4日消息,慢雾MistTrack监测显示,JPEG'd攻击者或已将全部6106.75枚ETH归还给项目方。[2023/8/4 16:18:46]
沿用刚刚的比喻,来看看群(group)这个数据结构是如何定义的。

由此可以推出许多有意思的定理:

举几个例子:

慢雾:区块链因黑客攻击损失总金额已超300亿美元:金色财经报道,据慢雾统计数据显示,自2012年1月以来,区块链黑客造成的损失总金额约为30,011,604,576.24美元;黑客事件总数达到1101起。
其中Exchange、ETH Ecosystem、Bridge是在黑客攻击中损失最大的类别,损失金额分别为10,953,323,803.39美元、3,123,297,416.28美元,2,005,030,543.30美元。另外合约漏洞、Rug Pull、闪电贷攻击是最常见的攻击方式,分别发生黑客事件137起,106起,87起。[2023/7/7 22:24:09]

拉格朗日定理
现在介绍一个非常有意思的定理,这个定理的推导在文末引用的视频中。
慢雾:近期出现新的流行恶意盗币软件Mystic Stealer,可针对40款浏览器、70款浏览器扩展进行攻击:6月20日消息,慢雾首席信息安全官@IM_23pds在社交媒体上发文表示,近期已出现新的加密货币盗窃软件Mystic Stealer,该软件可针对40款浏览器、70款浏览器扩展、加密货币钱包进行攻击,如MetaMask、Coinbase Wallet、Binance、Rabby Wallet、OKX Wallet、OneKey等知名钱包,是目前最流行的恶意软件,请用户注意风险。[2023/6/20 21:49:05]
“群的阶能被子群的阶整除。”
为什么说这个定理有意思呢,不仅仅因为它的证明过程串起了刚刚介绍的许多知识,还因为下面的结论:

慢雾:警惕高危Apache Log4j2远程代码执行漏洞:据慢雾安全情报,在12月9日晚间出现了Apache Log4j2 远程代码执行漏洞攻击代码。该漏洞利用无需特殊配置,经多方验证,Apache Struts2、Apache Solr、Apache Druid、Apache Flink等均受影响。Apache Log4j2是一款流行的Java日志框架,建议广大交易所、钱包、DeFi项目方抓紧自查是否受漏洞影响,并尽快升级新版本。[2021/12/10 7:30:00]
Ed25519 的实现
现在我们来讲 Ed25519,它是 EdDSA 算法的其中一种。EdDSA 有 11 个参数(https://datatracker.ietf.org/doc/html/rfc8032#autoid-3),这些参数的具体选择对于算法的安全和性能有很大的影响。Ed25519 的具体选择请参看链接(https://datatracker.ietf.org/doc/html/rfc8032#autoid-9)。
另外,值得一提的是这套算法用到了一个叫 Curve25519(https://datatracker.ietf.org/doc/html/rfc7748#autoid-5)的椭圆曲线。对于椭圆曲线,我们只需知道,它上边有很多很多点,这些点相加能得到新的点,新的点还是在曲线上。这些点和这个加法能形成一个群。注意这里的椭圆曲线加法(https://www.wikiwand.com/en/Elliptic_curve_point_multiplication)是有特殊定义的。
我们约定如下记法:

这是个交互式的算法,但是没关系,有一个技巧叫做 the Fiat – Shamir heuristic(https://link.springer.com/chapter/10.1007%2F3-540-47721-7_12),它可以把任意的交互式算法转化成非交互式的算法。最终我们会用非交互式算法。
数字签名算法都会给我们如下 API:

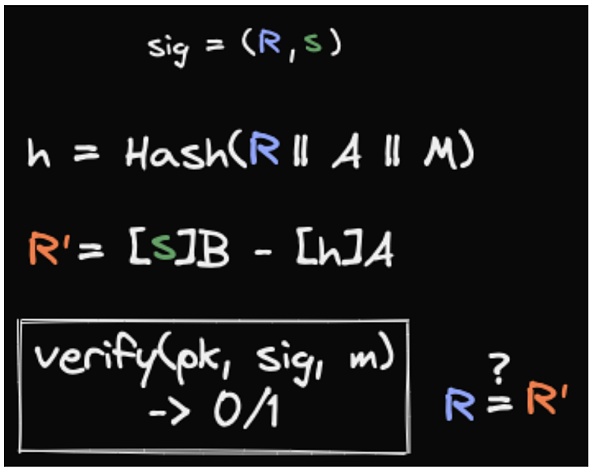

密码学算法的实现和使用都有非常多要注意的地方。当我们说一个数字签名算法是安全的,一般指的是即使在攻击者能够获得任意消息的签名(Chosen Message Attack)的情况下,攻击者仍然不能伪造签名。Ed25519 满足这个性质,但不代表 Ed25519 是绝对安全的。在原始的论文中也提到,可延展性问题是可以接受的,且原始的算法就有这个问题。
慢雾科技
个人专栏
阅读更多
区块律动BlockBeats
Foresight News
曼昆区块链法律
GWEI Research
吴说区块链
西柚yoga
ETH中文
金色早8点
金色财经 子木
ABCDE
0xAyA
郑重声明: 本文版权归原作者所有, 转载文章仅为传播更多信息之目的, 如作者信息标记有误, 请第一时间联系我们修改或删除, 多谢。